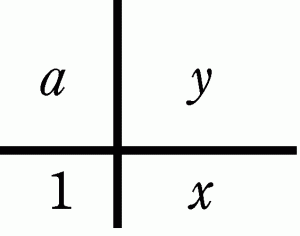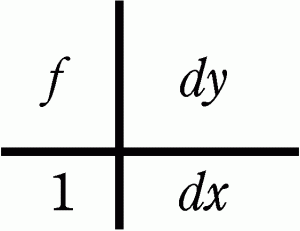学校を離れ、近所の子供たちの数学を見るようになって改めて痛感するのだが、割合や速度の計算を苦手とする子は多い。子供たちにどう教えようか模索しているうちに、この４ます図に出会った。（不勉強の至りである。）特に誰かの発明と言うより、様々な方が工夫し使ってこられたようである。一部の参考書に登場する。インターネット上にも様々なコメントがある。例えばこちら。また呼び名も様々、書き方も様々。一応整理してみる。

例１　一人３個ずつ、５人に、アメを配ると合わせて何個になりますか。 

これを、次のような表にする。

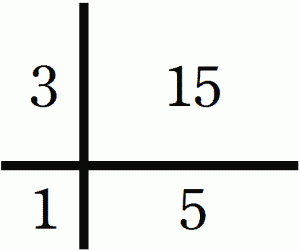この表記はかけ算の性質をよく表している。上の問で言えば
（一人あたりのアメの量）×（人数）＝全体のアメの量
単位で言うと
（個／人）×（人）＝（個）
３つの違った単位があらわれる。面積でも、実は
(m²/m)×(m)＝m²
なのだから。
この図を通して逆に３つの単位の関係を考えることができる。
同時に、割り算には２つの種類があることを、単純に表現してくれる。
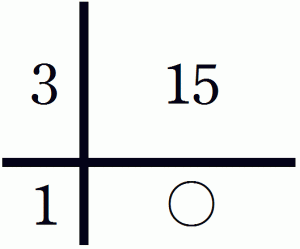
例１’１５個のアメを３個ずつ配ると何人に配ることができますか。

例１’’１５個のアメを５人で分けると一人あたり何個ですか。

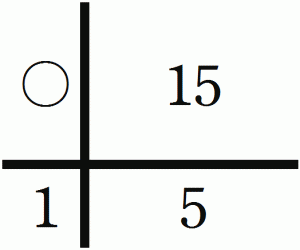この関係が小学校低学年でたたき込まれていれば、高学年で苦労することはないはずだ。
先のリンクにあった問題
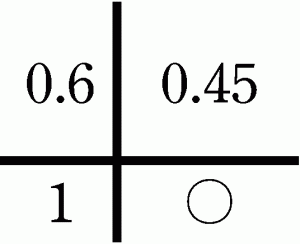
問題　畑１平方メートルに0.6Lの液体肥料をまきたい。肥料は0.45Lある。
何平方メートルの畑にまけるか。
図にできれば簡単に解ける。

この図はそのまま割合に移行できる。
例２　３の５倍はいくらですか。

割合計算が、かけ算の抽象化であることを図が教えてくれる。
まず整数値で習熟した後
例３　３００円は４００円の何倍ですか。

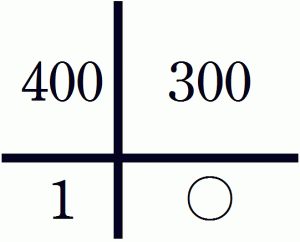速さについても同様
例４　１時間に３km歩くとき５時間で何キロ歩けますか。

速さを苦手にする生徒を見ていると、速度を割合だと考えているように思われる。割合は、同じ単位の二つの量の比だから、「時間」＝「割合」と教えるべきなのだ。田の字では、割合・倍の欄に時間が入る。

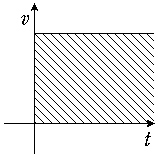
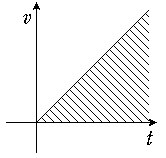
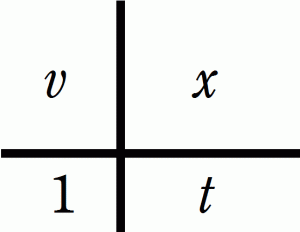高校の物理で移動距離を v-t グラフの面積で表わすことにつながる。
等速運動

等加速度運動

広く行われているT字による表現、いわゆる「はじき」は、３つの単位の関係を上手く表現しているとは言い難い。

中１で登場する正比例の関係は

微積分学の基本定理も図にするとこうなるだろう。

また、濃度の問題
例５　食塩２０gで８パーセントの食塩水を作ると全体の重さはいくらか。

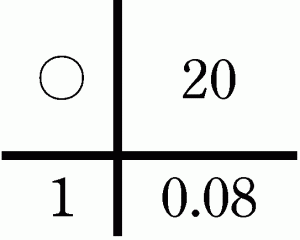このように、積に関する４マス図は、積の概念を一般的に表現してくれる。
左下の１に手を付ければ図は比例式一般をあつかうことができる。
２：６＝５：１５
は、４マス図で表現すれば、

このとき、６×５＝２×１５
斜めのかけ算は等しく、縦どうし、横どうしの割り算は等しい。
小学校２年の算数から、中学生の理科まで統一的にこの図で説明してくれたら、少しは理系離れが食い止められるのではないかと思うのだが如何だろう。

《追記》　エクセルでプリント　の項に『田の字表』を取り入れた作問ワークシートを追加。お試し下さい。私自身、小学校の算数でつまずいた中学生に使用して大変効率的でした。